III. Les graphes géométriques▲
Jusqu'ici nous n'avons vu que la génération des graphes, mais maintenant nous allons voir comment les utiliser avec une autre page et un formulaire.
Les graphes géométriques sont des courbes représentant des équations généralement à variable continue.
III-A. Courbe d'une fonction▲
Créons un petit formulaire pour que les utilisateurs puissent entrer la fonction qu'ils veulent tracer. Utilisons la méthode « POST » pour le formulaire et pour transmettre les données à la page qui va générer la courbe, nous passons la fonction à notre fichier qui génère le graphe en GET.
<html>
<head>
<title>Courbe</title>
<meta http-equiv="Content-Type" content="text/html; charset=ISO-8859-1">
</head>
<body>
<form method="POST">
fonction f(x) = <input type="text" name="fct" />
<input type="submit" value="Tracer"/>
</form>
<?php if(isset($_POST['fct']))
{
//Affiche la fonction à tracer
echo 'f(x) = '.$_POST['fct'].' <br />';
//appel de la page qui génère l'image en mettant la fonction en URL
echo'<img src="fonction.php?fct='.urlencode($_POST['fct']).'"/>';
}
?>
</body>
</html>Récupérons ensuite la fonction dans la page qui va tracer la courbe. Les simples utilisateurs ne sauront pas comment sont utilisées les variables en PHP et utilisent les notations de fonction standard (exemple f(x)=sin(x)*2) or PHP ne connait pas la variable x, nous devons alors transformer les x en $x. Dans le cas de l'exponentielle (exp(x)), il sera transformé en e$xp($x) ainsi il faut reconstituer.
Pour tracer la courbe d'une fonction y=f(x), il faut calculer la valeur de y à chaque déplacement de x et nous obtiendrons les coordonnées du point (x,y), calculer ensuite les coordonnées du point suivant et tracer une ligne qui joint les points consécutifs pour obtenir la courbe.
Attention !
L'utilisation de la fonction eval est déconseillée, surtout avec des données provenant d'un utilisateur. Ce code n'est qu'un exemple pour des tests.
<?php
header('Content-type: image/png');
//taille de l'image
$largeur=1000;
$hauteur=800;
//création de l'image
$courbe=imagecreatetruecolor($largeur, $hauteur);
//Allocation des couleurs
$bleu=imagecolorallocate($courbe, 0, 0, 255);
$blanc=imagecolorallocate($courbe, 255, 255, 255);
$rouge=imagecolorallocate($courbe, 255, 0, 0);
$trait=3;
//borne inférieure
$xmin=-10;
//borne supérieure
$xmax=10;
//Calcul des échelles
$echelleX=($largeur-10)/($xmax-$xmin);
$echelleY=$echelleX;
//déclaration de la variable globale pour la fonction
global $fct;
//affectation de la fonction passer en URL dans la variable
$fct=($_GET['fct']);
//Remplacer x par $x pour une variable php
$fct=str_replace('x', '$x', $fct);
//Remplacer e$x par ex pour la fonction exponentielle
$fct=str_replace('e$x', 'ex', $fct);
function f($x)
{
global $fct;
try
{
//evaluer la chaine fct pour avoir une instruction mathématique afin de calculer y
eval( "\$y = $fct;");
}
catch (Exception $exception)
{
$y=0;
}
return($y);
}
//Colorier le fond
imagefilledrectangle($courbe,0 , 0, $largeur, $hauteur, $bleu);
//Tracer les axes de l'abscisse et ordonnée
imageline($courbe, 0, $hauteur/2, $largeur,$hauteur/2, $blanc);
imageline($courbe, $largeur/2,0,$largeur/2,$hauteur, $blanc);
//Ecrire les graduations négatives de l'abscisse
$pasX=$largeur/2;
$i=0;
while($pasX>0)
{
//Ecrire la valeur
if($i!=0)
{
imagestring($courbe, 1, $pasX-$trait,$hauteur/2+10 , -$i, $blanc);
}
//Le petit trait
imageline($courbe, $pasX, $hauteur/2-$trait, $pasX,$hauteur/2+$trait, $blanc);
$pasX=$pasX-$echelleX;
$i++;
}
//Ecrire les graduations positives de l'abscisse
$pasX=$largeur/2;
$i=0;
while($pasX<$largeur)
{
if($i!=0)
{
imagestring($courbe, 1, $pasX-$trait,$hauteur/2+10 , $i, $blanc);
}
imageline($courbe, $pasX, $hauteur/2-$trait, $pasX,$hauteur/2+$trait, $blanc);
$pasX=$pasX+$echelleX;
$i++;
}
//Ecrire les graduations négatives de l'ordonnée
$pasY=$hauteur/2;
$i=0;
while($pasY>0)
{
if($i!=0)
{
imagestring($courbe, 1, $largeur/2-10,$pasY-3 , $i, $blanc);
}
imageline($courbe, $largeur/2-$trait, $pasY, $largeur/2+$trait, $pasY, $blanc);
$pasY=$pasY-$echelleY;
$i++;
}
//Ecrire les graduations positives de l'ordonnée
$pasY=$hauteur/2;
$i=0;
while($pasY<$hauteur)
{
if($i!=0)
{
imagestring($courbe, 1, $largeur/2-14,$pasY-3 , -$i, $blanc);
}
imageline($courbe, $largeur/2-$trait, $pasY, $largeur/2+$trait, $pasY, $blanc);
$pasY=$pasY+$echelleY;
$i++;
}
//Traçage de la courbe
$j=false;
$pas=0.01;
$xmin=-10;
$xmax=-$xmin;
while($xmin<$xmax)
{
//Calculer l'ordonnée du point
$y=round(-f($xmin)*$echelleY)+($hauteur/2);
if($j)
{
//Joindre le point présent avec la précédente
imageline($courbe,round(($xmin-$pas)*$echelleX)+($largeur/2),$yprev,round(($xmin)*$echelleX)+($largeur/2),$y,$rouge);
}
$j=true;
//Sauvegarder l'ordonnée du point actuel
$yprev=$y;
$xmin+=$pas;
}
//Envoie du flux de l'image
imagepng($courbe);
imagedestroy($courbe);
?>III-B. Courbe représentant une équation polaire▲
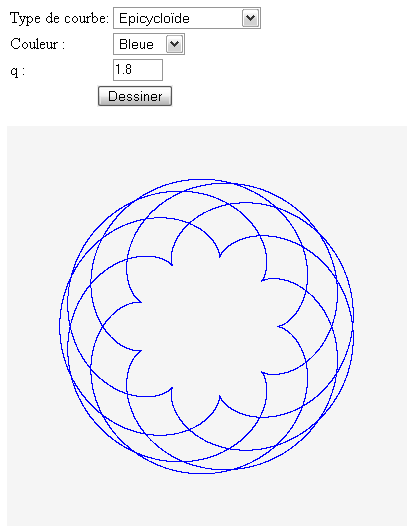
Pour tracer une courbe d'une équation polaire, nous utilisons une paramétrisation cartésienne pour faciliter la tâche, c'est-à-dire utiliser deux équations, l'une pour calculer x et l'autre pour calculer y en fonction de l'angle thêta pour obtenir les coordonnées d'un point(x,y). Nous prenons comme exemple les cas des épicycloïdesépicycloïdes et hypocycloïdeshypocycloïdes. Une hypocycloïde et une épicycloïde ont la même équation, mais seulement le paramètre q de l'hypocycloïde prend la valeur négative de celui de l'épicycloïde.
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.01 Transitional//EN">
<html>
<head>
<title>Dessin</title>
<meta http-equiv="Content-Type" content="text/html; charset=ISO-8859-1">
<?php $st='selected="selected"'?>
</head>
<body>
<form method="POST">
<table>
<tr>
<td>Type de courbe:</td>
<td>
<select name="type">
<option value="2" <?php if(isset($_POST['type'])&& $_POST['type']=="2") echo $st;?>>Epicycloïde</option>
<option value="3" <?php if(isset($_POST['type'])&& $_POST['type']=="3") echo $st;?>>Hypocycloïde</option>
<option value="4" <?php if(isset($_POST['type'])&& $_POST['type']=="4") echo $st;?>>Epi&Hypo-cycloïde</option>
</select>
</td>
</tr>
<tr><td>Couleur :</td>
<td>
<select name="couleur">
<option value="1" <?php if(isset($_POST['couleur'])&& $_POST['couleur']=="1") echo $st;?>>Bleue</option>
<option value="2" <?php if(isset($_POST['couleur'])&& $_POST['couleur']=="2") echo $st;?>>Rouge</option>
<option value="3" <?php if(isset($_POST['couleur'])&& $_POST['couleur']=="3") echo $st;?>>Verte</option>
</select>
</td></tr>
<tr>
<td >q : </td>
<td>
<input type="text" name="k" size="4" <?php if(isset($_POST['k']))
{echo ' value="'.$_POST['k'].'"';}
else {echo ' value="1.8"';} ?>/>
</td>
</tr>
<tr><td colspan="2" align="center"><input type="submit" value="Dessiner"/> </td></tr>
</table>
</form>
<?php if(isset($_POST['type']))
{
echo'<img src="dessin.php?type='.$_POST['type'].'&q='.$_POST['k'].'&couleur='.$_POST['couleur'].'"/>';
}
else
{
echo'<img src="dessin.php?type=2&q=1.8&couleur=1"/>';
}
?>
</body>
</html><?php
header('Content-type: image/png');
$largeur=400;
$hauteur=400;
$courbe=imagecreatetruecolor($largeur, $hauteur);
$fond=imagecolorallocate($courbe, 245, 245, 245);
imagefilledrectangle($courbe,0 , 0, $largeur, $hauteur, $fond);
if(isset($_GET['type'])&& !empty ($_GET['type']))
{
$type=$_GET['type'];
if($_GET['couleur']=="2")
{
$couleur=imagecolorallocate($courbe, 255,0, 0);
}
else{
if
(
$_GET['couleur']=="1"){$couleur=imagecolorallocate($courbe, 0,0, 255);
}
else
{
$couleur=imagecolorallocate($courbe, 0,255, 0);
}
}
$q=$_GET['q'];
eval( "\$q = $q;");
switch ($type)
{
//Epicycloïde
case '2':
{
$xmin=-8*M_PI;
$xmax=8*M_PI;
$echelleX=70;
$echelleY=$echelleX;
while($xmin<($xmax)) {
$x=(($q+1)*cos($xmin)-(cos(($q+1)*$xmin)))/$q;
$y=(($q+1)*sin($xmin)-(sin(($q+1)*$xmin)))/$q;
imagesetpixel($courbe,round($x*$echelleX)+($largeur/2),round(-$y*$echelleY)+($hauteur/2),$couleur);
$xmin+=0.001;
}
break;
}
//Hypocycloïde
case'3':
{
$xmin=-8*M_PI;
$xmax=8*M_PI;
$echelleX=70;
$echelleY=$echelleX;
while($xmin<($xmax)) {
$x=(($q-1)*cos($xmin)+(cos(($q-1)*$xmin)))/$q;
$y=(($q-1)*sin($xmin)-(sin(($q-1)*$xmin)))/$q;
imagesetpixel($courbe,round($x*$echelleX)+($largeur/2),round(-$y*$echelleY)+($hauteur/2),$couleur);
$xmin+=0.001;
}
break;
}
//Superposition d'une Hypocycloïde et Epicycloïde
case '4':
{
$xmin=-8*M_PI;
$xmax=8*M_PI;
$echelleX=70;
$echelleY=$echelleX;
while($xmin<($xmax)) {
$x=(($q+1)*cos($xmin)-(cos(($q+1)*$xmin)))/$q;
$y=(($q+1)*sin($xmin)-(sin(($q+1)*$xmin)))/$q;
imagesetpixel($courbe,round($x*$echelleX)+($largeur/2),round(-$y*$echelleY)+($hauteur/2),$couleur);
$x=(($q-1)*cos($xmin)+(cos(($q-1)*$xmin)))/$q;
$y=(($q-1)*sin($xmin)-(sin(($q-1)*$xmin)))/$q;
imagesetpixel($courbe,round($x*$echelleX)+($largeur/2),round(-$y*$echelleY)+($hauteur/2),$couleur);
$xmin+=0.001;
}
break;
}
}
}
imagepng($courbe);
imagedestroy($courbe);
?>III-B-1. Capture d'écran▲
IV. Conclusions▲
Nous avons pu voir comment utiliser la bibliothèque GD pour créer quelques graphes statistiques, mais il en manque encore d'autres comme le diagramme de fréquence, la toile d'araignée, les pyramides d'âges, etc. Ces autres diagrammes se basent sur les mêmes principes que les exemples que nous avons pris dans cet article. Par exemple pour les diagrammes de fréquence du suivi des ventes d'un produit au cours d'une année, il suffit de calculer la quantité vendue en un mois sur la quantité de vente totale durant l'année.
V. Remerciements▲
Mes remerciements à RideKick pour la relecture de cet article.